Fixing the old folgezettel
For context, please see the two other posts. Here's the first one, and here's the second one. You'll see how the thinking evolved from these posts.
I had a conversation with @ctietze about the Folgezettel technique.
He told me that there are two problems with the current branching method of the Folgezettel, as follows:
- The binary tree nature of it
- The proximity problem
He discussed these issues with me with great detail (even though I asked for a short answer) and I'm really grateful that he spent the time to do so. According to him, two branching issues has been a great limitation of the Folgezettel technique, and perhaps they're all the more reason Christian and Sascha don't advocate it.
Anyway, the bigger trap here is that these two problems don't surface until you've worked with your Zettelkasten for a while; you could end up wasting serious amounts of time once they do. In Christian's words,
It's still limited, but the limits surface later. It's also still suffering from the same design problems: the beautiful tree of today will be torn apart tomorrow, and you have no way of getting back to the associations of today's tree without taking note of it, too.
I strongly agree—I wouldn't have found it if I didn't do any thought experiments and real ones using a mock collection. And that's only for the first problem. Christian pointed out the second problem before I can even find it. Nonetheless, developing a potential solution comes from solving these two major branching problems at once.
(The hierarchy problem was solved already, so I'm going to skip that out for a bit. Short, contextual summary: "1" and "1a" shouldn't be treated as a parent-child relationship, but rather as a sibling relationship. Hierarchies could happen, but not exclusively so)
Why worry about Folgezettel, anyway?
Some of you might think I'm too crazy to even create a couple of discussions about a seemingly outdated technique. But I get it. @sfast has already debunked much of the arguments for the Folgezettel.
But I tried keeping a UID-system and I found it hard to maintain it using structure notes alone. Of course, that's just me. And that's why I care about reviving this old technique. My thinking was, "If Luhmann can use this flawed technique to work with 90,000 physical notes, then perhaps I can modify this one to make it work better in a digital system."
My hypotheses is that:
It lessens the dependence on structure notes, because the notations _supposedly make it easier to find connections just within your list. (more on "supposedly" later)_
That said, I still find value in using structure notes in my system--that's undeniable. For example, when I form relationships from the branch 1a to 1a1a1a and the branch 1b to 1b1a1a through a direct link, I get a relationship of relationships. (Let's call that: relationship^2)
These relationship^2 almost always emerges an interesting topic. And since this connection isn't intuitive at first glance, structure notes help elaborate these connections.
Anyway, this post will tell you how I came up with Note Sequence 2.0 (for a lack of a better name)--a modified version of the Folgezettel technique that allows you to:
- See all succeeding notes easily. Just by putting its notation in the search bar, you can see all of the notes that follow it, even in the second-, third-, fourth-, or n-th order.
- Use Folgezettel like a mind map. In the binary tree problem section, I discussed how branching is way limited using the old folgezettel. Thus, instead of working like a real web of notes while maintaining the usefulness of the notations, it only works like a fork in a road.
- Avoid losing proximate notes. The old folgezettel defeats its own purpose when, say, 1a and 1b eventually contain a lot of notes in between. If we take the assumption that 1a is connected ONLY (through notation) to 1a1 and 1b, then the purpose of "being able to quickly see connected notes through notations alone" becomes defeated.
- Not depend on visualization scripts to see connections. This only applies to notated notes, though. You'll see what I mean later.
I hope I'm making sense. So let's start with the first problem.
The binary tree problem
Explained simply, _binary _means two states, but applied in branching, it means you can only branch out two times.
See, the method of Folgezettel described in niklas-luhmann-archiv.de looks like this:
1.1 Sticky note
- 1.1a Connection to a term at 1.1
- 1.1a1 Connection to a term at 1.1a
- 1.1a2 Continuation of the sticky note from 1.1a1
- 1.1a2a Connection to 1st term at 1.1a2
- 1.1a2b Connection to 2nd term on 1.1a2
- 1.1b Continuation of the note from 1.1a
1.2 Continuation of the note from 1.1
This was the exact method reportedly used by Luhmann. But when I started working on it (after not thinking about @sfast's arguments well enough), I stumbled upon what we call the binary tree problem.
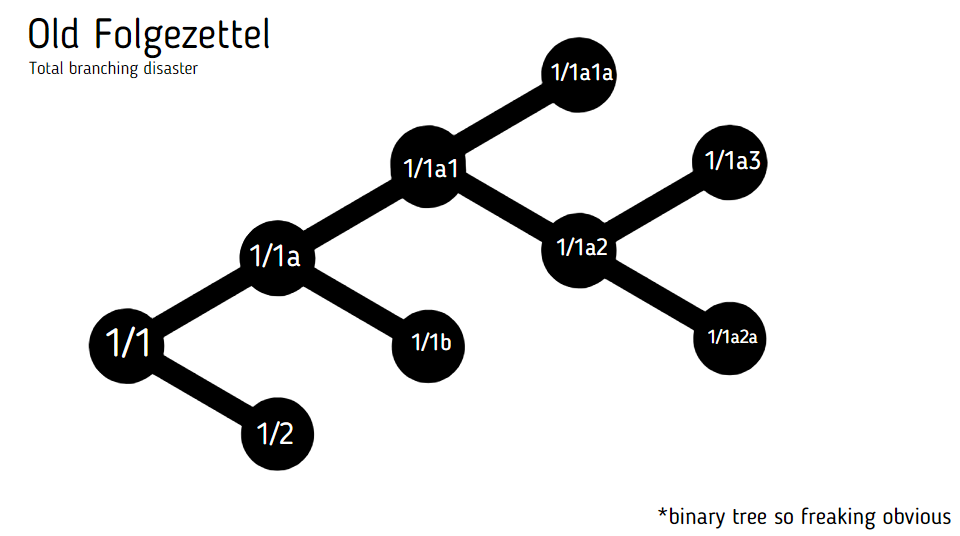
For example, if you have note 1/1, 1/2, and 1/1a, that means you've already branched the note 1/1 two times. What happens if you stumble upon an idea that also connects to 1/1? That's right, it's damned because 1/1 ain't so gregarious.
Here's a visualization. (Please don't mind the ugly faces; they helped me survive graphic creation I hate so much)
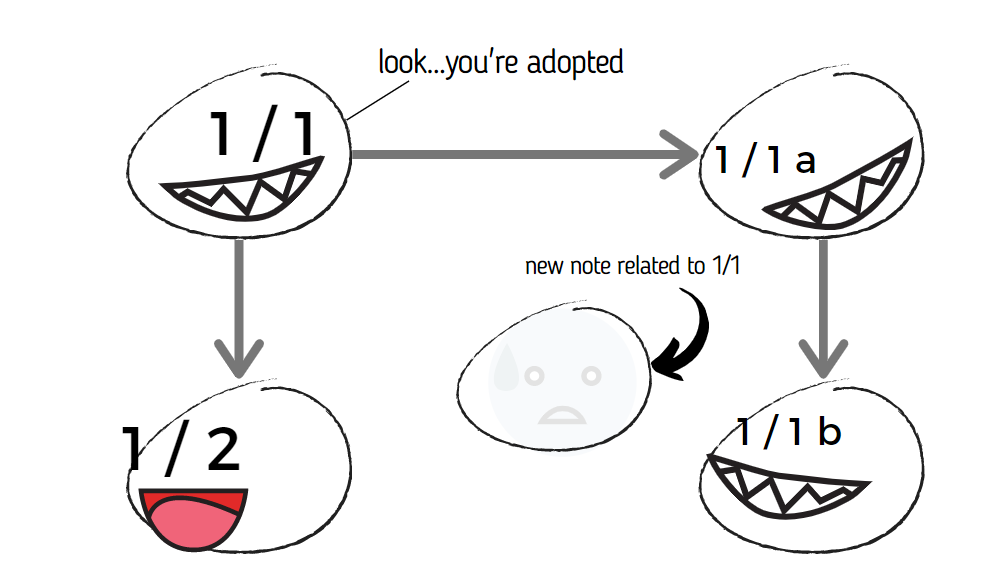
If you make it a rule to continue 1-1 using 1-2 and 1-1a only, you'd encounter the binary tree problem:
A note with two Folgezettels already cannot be continued by another Folgezettel.
You can get creative to solve the binary tree problem like I did: "just create a new note sequence, then connect them together" — but that defeats the purpose of the Folgezettel (recall: to easily see the flow of your ideas right at the file list). You might as well use UID's.
(WAIT don't get me wrong, I DO see the value in the UID system and I'm not discrediting it just because I'm developing a seemingly "opposed" technique. I just wanna get that out of the way. UID's and Structure Zettel are proven methods to organize a Zettelkasten. Anyone who attacks that argument will get burned slowly by afternoon sunshine.)
But let's say you somehow tried to solve the binary tree problem by using a different character set for a suffix. 1/1a and 1/2 are already taken, right? It would look like this:
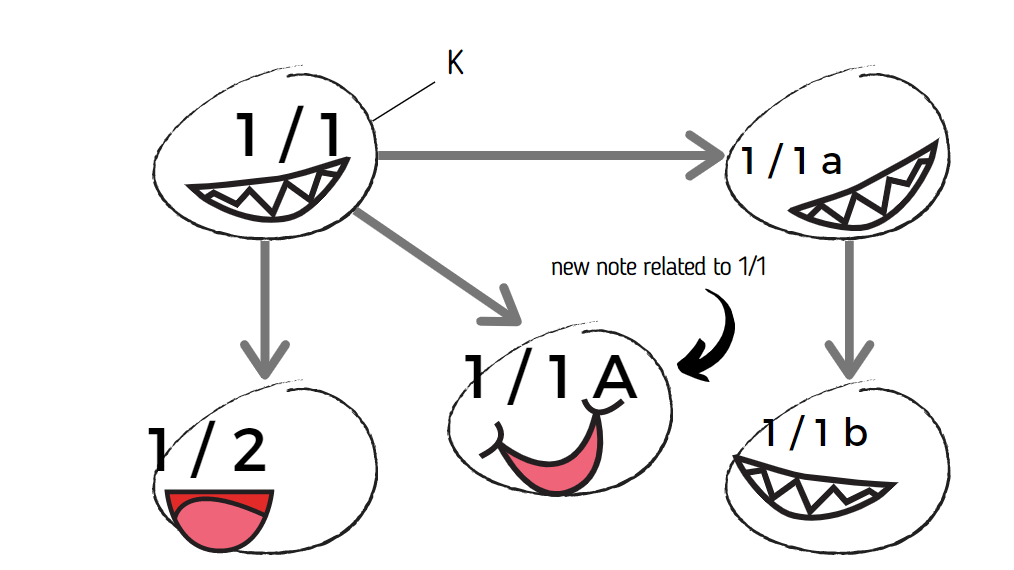
Okay, but how long can you do that? Four times, using:
- a small letter, which is taken already
- a capital letter
- another number, which can be confusing to look at
- a special character, if you're quite sadistic
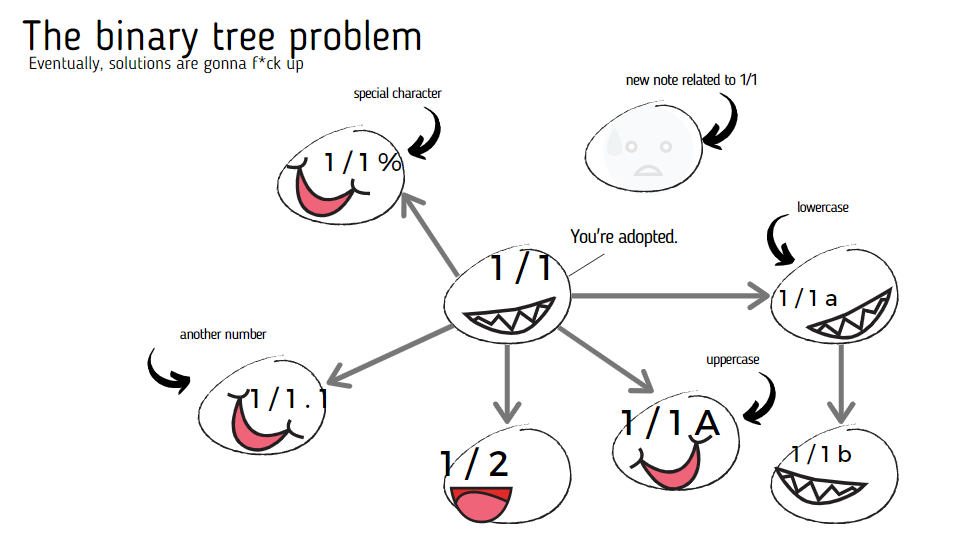
Clearly, as long as you incorporate a binary tree using the Folgezettel, the limited branching problem is inevitable.
Therefore, my solution is, if you want to make sense using the Folgezettel, instead of only having binary trees, I have to make it work such that we have a multiary tree. (Branching multiple times)
Coherently, the brain isn't binary—it's also multiary. One thought leads to many other thoughts. It wouldn't make sense to use the binary tree structure of the Folgezettel. But we will get to that later. Let's move on to the next problem.
The Proximity Problem
The proximity problem is like the son of the binary tree problem. Except it happens between two already linked notes in a Folgezettel.
See, if we accept the assumption that 1/2a is linked to 1/2b, then all the further connections of 1/2a will only push 1/2b further down. This is how it looks like:
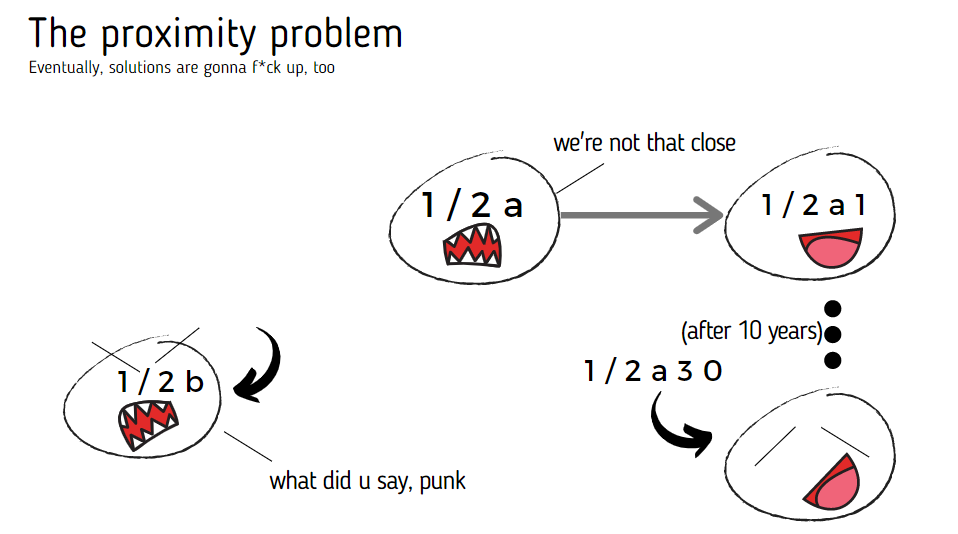
I've found solutions for this online, but it doesn't really solve the problem at its root. Again, this defeats the purpose of the Folgezettel since you want to see the continuation of your ideas right away.
"But we're using digital tools now!" Alright, I get it. But hey, we haven't even solved the first problem yet.
If we want to use the Folgezettel digitally and make it work like the brain, then we have to remodel it such that these two problems don't exist.
Note Sequence 2.0
First off, if we follow the assumption that:
1.1 Sticky note
- 1.1a Connection to a term at 1.1
- 1.1a1 Connection to a term at 1.1a
- 1.1a2 Continuation of the sticky note from 1.1a1
- 1.1a2a Connection to 1st term at 1.1a2
- 1.1a2b Connection to 2nd term on 1.1a2
- 1.1b Continuation of the note from 1.1a
1.2 Continuation of the note from 1.1
…as prescribed in the main website niklas-luhmann-archiv.de, then the binary tree problem becomes inevitable. It is the root of our problem here--THIS prescription is what make Folgezettel limited to a binary tree.
Just to quote Sascha, "Should you use a technique just because Luhmann did it?" my answer is no. That might sound contradictory because I'm using Folgezettel, but this isn't copying Luhmann—I'm improving upon what he did.
With that out of the way, let's ditch that old, flawed technique (Sorry, Niklas) and let's change the rules into this:
1.1 Sticky note
- 1.1a Connection to 1.1
- 1.1a1 Connection to 1.1a
- 1.1a2 Connection to 1.1a
- 1.1a2a Connection to 1.1a2
- 1.1a2b Connection to 1.1a2
- 1.1b Connection to 1.1
1.2 Not related at all
But if we adopt that notation, then the first number originally designated for the "note sequence number" actually becomes useless since 1.1 and 1.2 isn't related anymore. (Don't be confused with 1.1 and 1/1--they're the same) We can simplify it to:
1 Sticky note
- 1a Connection to 1
- 1a1 Connection to 1a
- 1a2 Connection to 1a
- 1a2a Connection to 1a2
- 1a2b Connection to 1a2
- 1b Connection to 1
2 Not related at all
And just by changing that, we actually solved the two problems at once.
- The branching is multiary. Any note related to 1 can become 1a, 1b, 1c, 1d...and so on. You can even extend the functionality by making 1-aa,1-ab,1-ac, until you read 1-zz. I believe that allows for 676 branches, and 99 branches when you use numbers. Either way, I doubt you can use them up, it's not likely to happen in practice. I'm inclined to believe using the notation 1a01a is enough as it allows 26 branches for letters (i.e. 1a01b, 1a01c, 1a01d...1a01z) and 99 branches for numbers (1a01a01, 1a01a02...1a01a99).
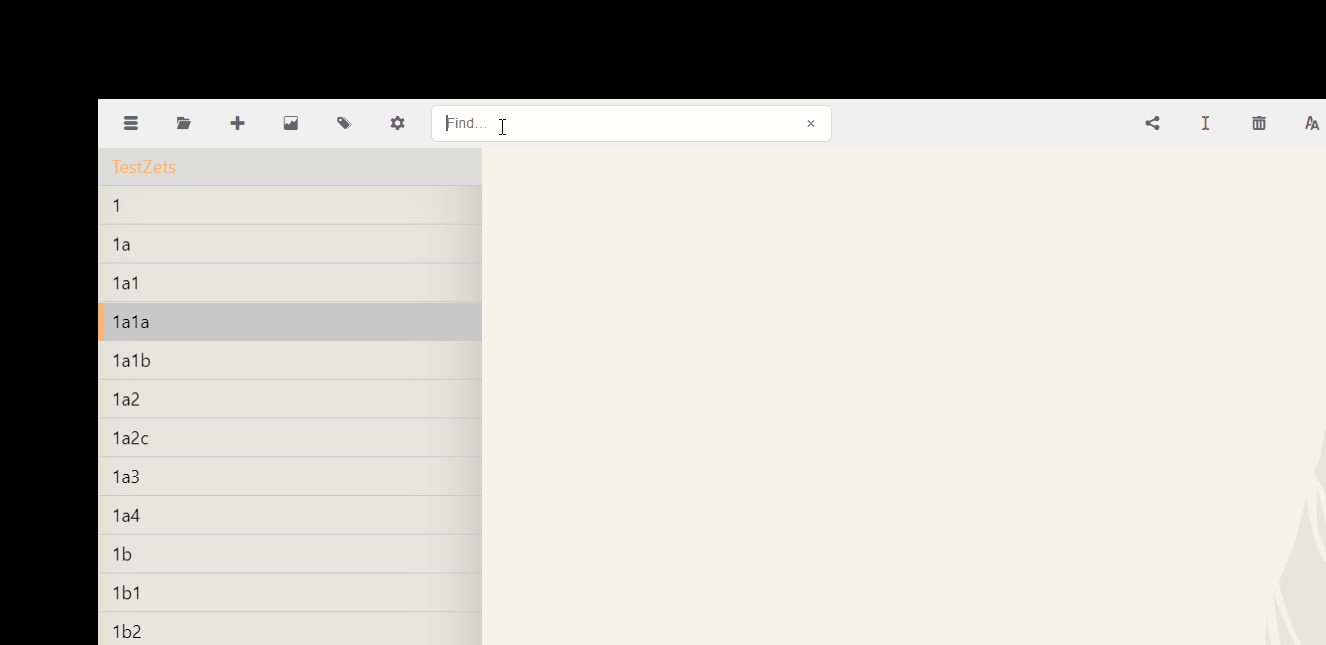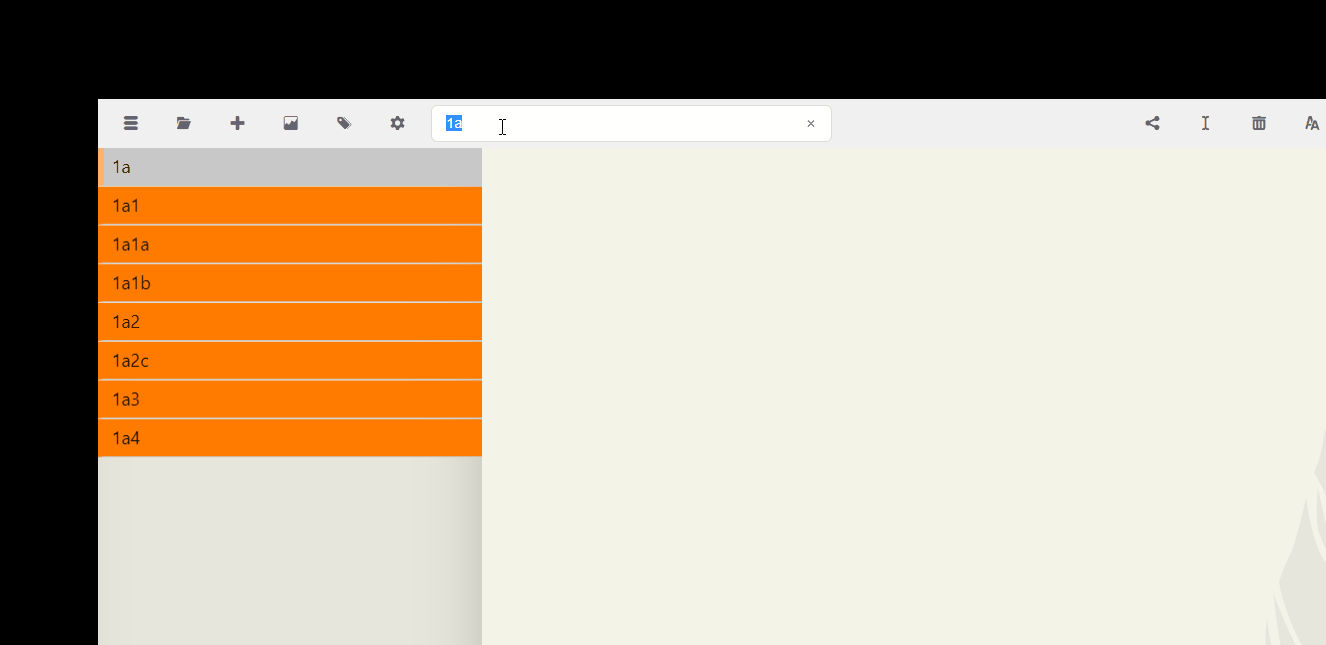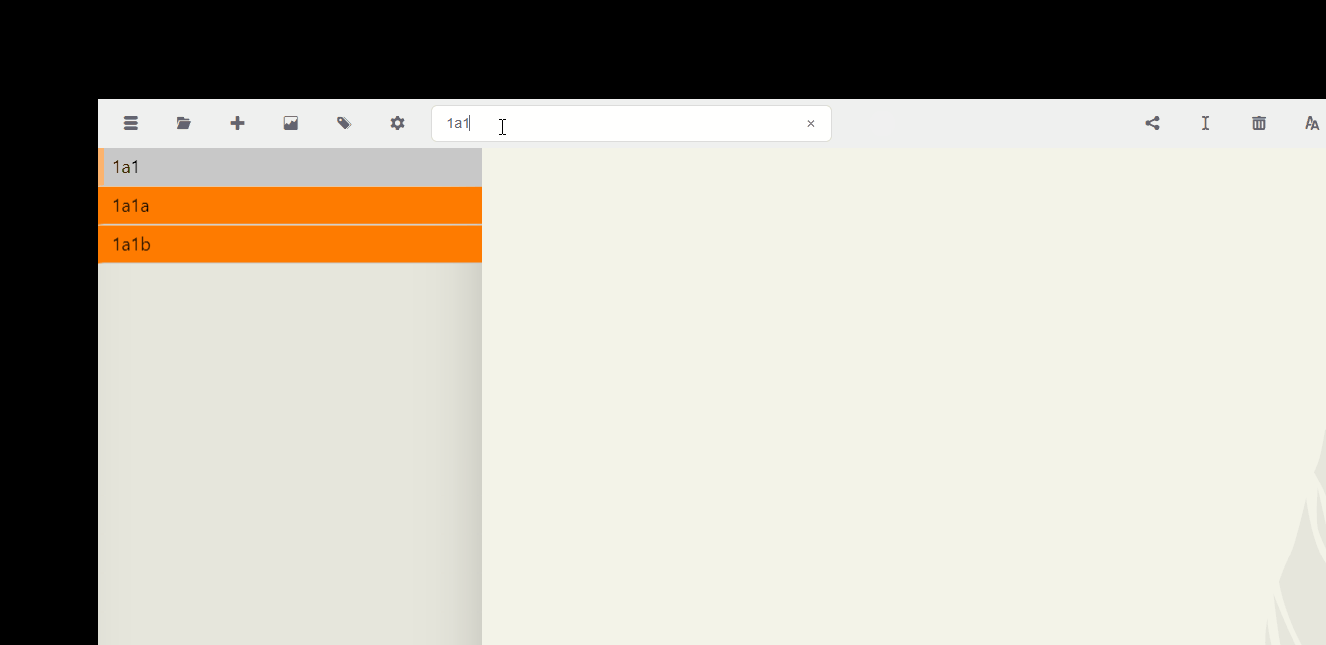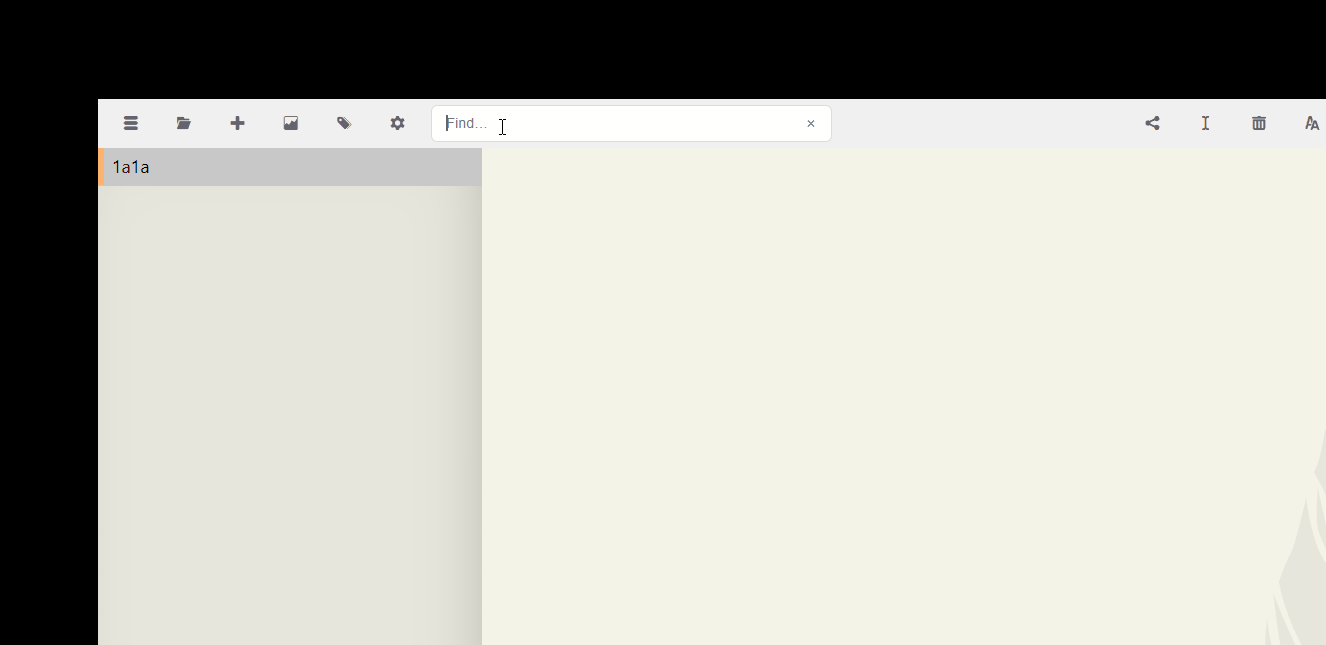
- Proximity doesn't matter anymore. Just by typing the characters in the search bar, you can easily find what follows a link. For example, typing 1a shows everything that follows 1a. To make this easier to process, let's review first.
In the old version, only 1a1 and 1b follows 1a; that sucks. Here's what it looks like:
In the new version, what I did was this:
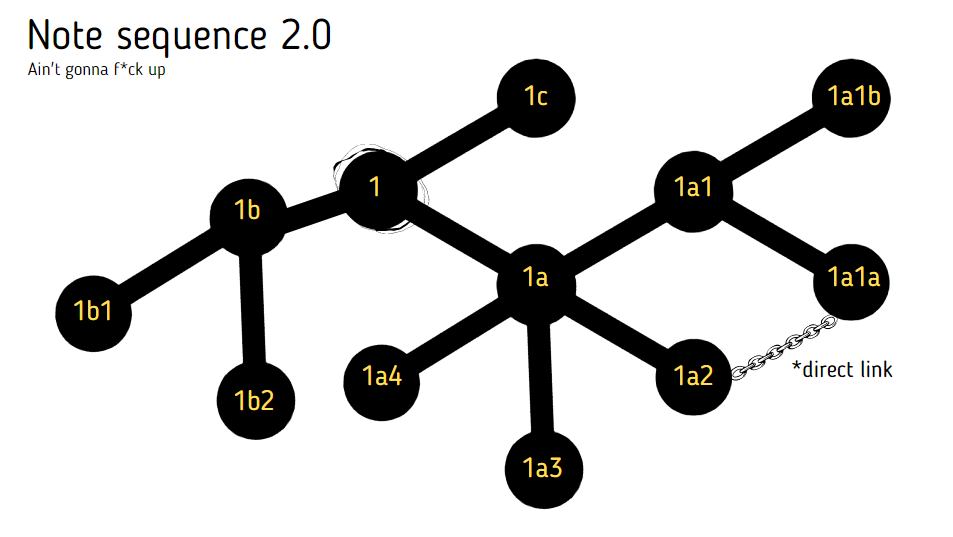
(Note: Please don't mind that I put direct links in this one. Both can have direct links.)
So far here's what I've accomplished by breaking the governing rules for the technique:
First, as promised, Note sequence 2.0 made it easier to search for connections through search. Searching for a note automatically shows you what comes next, albeit using the alternating letter-number scheme limits the number of branches you can make. Again, you can extend this functionality however you want, perhaps by using 1-a-01-a; it allows you to use letter branches 26 times, and number branches 99 times. Here's a visualization:
(See the Note Sequence 2.0 image above for reference)
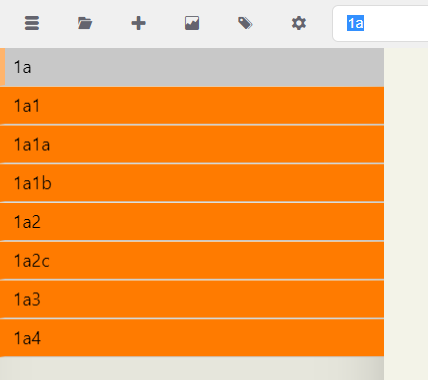
As you can see, searching for 1a makes it easy to see what follows it in the notated sequence. Let's try that for 1a1.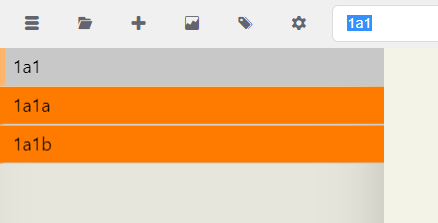
And then for 1b.
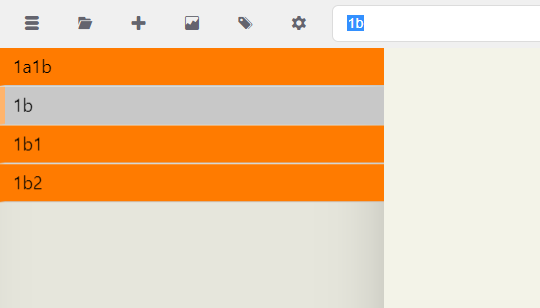
You might say that the last one also showed another note that has "1b" in it, and therefore "this doesn't work." Nope. It still makes it easy to see what follows 1b.
And second, avoiding the connection between 1-2-3-4 as well as 1a-1b-1c and so on allowed us to kill the binary tree problem and the proximity problem at once.
"No, you didn't solve the proximity problem!"
It seems that way, but then using search actually allows you to navigate through all proximate notes smoother than before. If you use the old Folgezettel, searching for 1a would NOT make 1b appear in the first place, much less notes that follow it (1c, 1d, 1d1, 1e, etc.).
Using 2.0, however, typing a notation (say, 1a) reveals ALL the following notes. All you have to do is type the next characters.
One caveat I found is that you can't use this method for Physical Collections anymore. Well, I guess none of you would do that, tho.
P.S. I'm yet to create a comprehensive post on the new Folgezettel technique (i.e. what principles it followed, what underlying assumptions/rules are) because of grad school. Sorry for that, but I hope this will suffice.
Howdy, Stranger!

Comments
@improveism thanks for expounding on your idea for Note Sequence 2.0. I must confess, having never utilized Luhman numbers (and obviously not paying close enough attention to the diagrams and examples, lesson learned!), I did not understand how they worked. I assumed that they were hierarchal (since I tend to think in outlines myself). But as you made clear in this post, that was not the case (side note: with an accurate understanding of the folgezettel numbering, I personally would not use such a numbering system).
Be that as it may, I now understand your 2.0 proposal more clearly: utilize a numbering scheme that is essentially hierarchal. I batch created 1800+ files to see how it scales, and it does indeed scale.
That said, although your proposal does indeed seem to solve both problems (great job! and having the search results populate is quite satisfying!), utilizing folgezettel in a hierarchal manner seems rather like a structure note without the possibility of comments unless making an actual structure note. Moving from continuation (a la, folgezettel) to connection (a la, structure note) makes this proposal seem less like a digital implementation/improvement upon folgezettel (or thought trains as others have called them), but more akin to embedding the concept of structure notes into the file name to create hierarchy and structure. How does this capture sequences of thought (in contrast to hierarchal structures of thought) if it's hierarchal? Unless I'm misunderstanding (again), your proposal actually seems to conceptually argue for structure notes over folgezettel. Perhaps I'll have to wait for you to explain the principles, rules, etc. in more detail. Thanks, again, though, for taking time to clarify your proposed method.
Hmm, you can say it that way, too. But more importantly:
My idea is that using 2.0, you won't have to create Structure Zettel for more conspicuous thought trails. You can choose to, but it's not going to feel as vital compared to UID-based systems. Put another way, using 2.0 you now only use Structure Zettel (in another level of Folgezettel, say A1, then A1a, then A1a1, for example) to explain the non-conspicuous connections in your collection--especially those with hierarchies! (They're a pain in the ass without Structure Zettel)
I can't explain it clearly yet, but I find that I'm having a hard time maintaining a UID-based system myself. I don't exactly know how the more experienced guys do it. I'm kinda having OCD to organize everything when I'm using it. But that's me. (Ironically, I gave myself a harder time to make this thing usable)
To summarize, Note Sequence 2.0 lessens the dependency on Structure Zettel, (or maybe urgency is the right word) and allows you to easily navigate through your entire collection without requiring visualization scripts and the like.
I love your demonstration! You nailed it. For others reading this, let me clarify that the notation might be hierarchical, but the content shouldn't always be that way. I feel like I should give this technique another name to somehow avoid the associated "hierarchical" property.
I’m having a hard time seeing the difference here but I also dig @improveism’s ideas so I’m trying to.
In my use of folgezettel I just use numbers.
So notes 1,2,1 and 1,2,2 are both notes that elaborate on note 1,2 but don’t elaborate on each other. If 1,2,2 was actually related to/elaborating on 1,2,1 I would make it 1,2,1,1.
If I have a new note that elaborate on 1,2,1 but not these other notes, it would become 1,2,3.
This still seems hierarchical by comparison to yours, but this solves the binary problem. At each level there are infinite branches possible.
This sounds similar, except I'm concurrently using letters and numbers.
But this one I can't grasp quite well. How does the actual topology look like?
I mean, if 1,2,2 and 1,2,1 aren't connected to each other, why is 1,2,3 connected to 1,2,2? I'm curious about the logic behind it.
Maybe I expressed that wrong. 1,2,3 is another elaboration on 1,2 (like 1,2,1 and 1,2,2). It’s a third dimension to note 1,2 that is not a direct elaboration on either 1,2,1 or 1,2,2.
YEAH that is exactly the same as the one I'm describing, except my notation follows a number with a letter (for frivolous reasons). Awesome So you were actually the first to have this idea. I recall you have 12,000+ notes using digital folgezettel, but I didn't figure you were already using this "2.0" thing I've randomly named for a lack of a better term.
So you were actually the first to have this idea. I recall you have 12,000+ notes using digital folgezettel, but I didn't figure you were already using this "2.0" thing I've randomly named for a lack of a better term.
How has your knowledge work gone so far?
The problem I see with this approach is that it does not include what luhmann called “ multiple storage“.
I still think the ludecke approach is superior, where you have a dedicated sidebar that tracks note sequences independently, allowing one note to be part of multiple sequences, which this numbering approach does not
@improveism , I understand that you are aiming to refine and improve your explanation, and many people here have found your comments very useful! I want to mention that posting revised content and pointing others to the previous posts for context does have a significant downside on a forum, which is that all of the other people's comments and unanswered questions are not carried forward, and if you have not addressed those in the new post, they are lost to the world.
One example of an idea raised in previous threads that has been lost in your latest revision, as far as I can tell. I asked why you think that allowing only 2 branches is a problem. I haven't seen an answer that was clear to me. @ctietze stated in a post in another thread that he thought the 2 branch limit was potentially a problem if the user wanted to see certain notes displayed visually near each other in space - what he calls the "proximity" issue. Is there any other issue that you think exists with a 2 branch limit? If so, can you explain it? If not, can you confirm that this problem you see with Luhmann's original system is potentially losing visual proximity of related note titles, and that is the issue you are aiming to solve?
Now, as far as solving this potential downside, here is my question: how can any proposed ID system with a coded content/structure-indicator in the title every overcome, even in theory, the proximity problem? You don't have to restate your earlier explanations - I got them. But there will always be some spatial limit on how many note titles can be "near" each other to be visually scanned , and no matter what ID scheme you use, that number won't increase. So the user will just hit that limit based on more child branches or fewer child branches. Or is that wrong? Is there some difference in the way that notes are displayed such that more branches will overcome the proximity problem? ( @ctietze , I'd love your answer to this as well)
Getting back to my first comment, may I request that you post revisions to your system in the original threads rather than create new threads whose firsts posts are revisions of substantially similar older posts? (I understand that the new ones may have important revisions.) Perhaps post a link to a revised article on a separate blog or website? It would help me, at least, follow the discussion and reduce the need for repeating content (including my own) in other threads. Thanks!
Can you explain what you mean with "coded content/structure-indicator"?
Author at Zettelkasten.de • https://christiantietze.de/
Yes, there's no short way to say it, I guess. With Luhmann IDs, each alphanumeric character is a sort of code or shorthand for content, structure, or both. So if the first topic in my ZK is 'Zettelkasten' then an LID that starts with
1indicates in some way a general topic. And an LID that contains1a2b2aindicates or conveys something about the structural placement of the note.Similarly, DTIDs encode (very clearly) the date/time the note was created.
So my point is that if a UID indicates something about note content or a note's structural position, then scanning a list of such notes gives you information that might be relevant for your current task, and once you have more than 100 notes you will start to hit a display limit for how many notes can be shown "proximately" to each other. But it's not clear to me why it would if the visible note limit (say 40 visible notes) is divided between 2 branches or 5.
Let me know if I misunderstood the "proximity problem".
(Proximity of note A and B: their being close to each other. Adjacent notes are closest. Greater distance, e.g. lines in a file listing, means reduced proximity; proximity and distance have an inverse relationship.)
If my layperson parsing of your statement is correct, I think we're on the same page: I think it does not matter how many dimensions of branching you include, because when only 40 notes fit on a page on the screen, and you want to see the note at the top of the screen and the note at the bottom of the screen at once, you cannot add a 41st note in between them. If you do, you cannot ever see them on the same page again. Having 10 ways to branch off of a note will still fail for the same reason that 2 ways to branch off fail. You run out of space on the page, and subsequent additions will push what previously were neighbors further apart.
via https://en.wikipedia.org/wiki/File:Sorted_binary_tree_ALL.svg
In a tree structure, siblings are still closer together in principle. Here, B and G would be siblings, both children of F. They only have 2 steps (B → F → G = 2 steps) between each other. But in a linear sequence of list rendition, you might have
... which shows 4 lines between B and G (if you change the sort order and G was at the top, there'd still be 2 lines in between).
The "perfect" rendition of sibling-ness is A/D and C/E, I think. They are next to each other in the list.
In outliners, you can fold child elements and see siblings close together:
▼ F ▶ B ▼ G ▼ I - HWhen you cannot hide portions in between the stuff you want to view in succession (e.g. via folding), you eventually will not be able to still look at the same stuff on a single page anymore.
Adding more stuff to "B" and its child nodes makes it impossible to see them on the same page ever again; the way you are allowed to add nodes in between (X-dimensional branching or confining the structure to a binary tree) doesn't matter.
Is this what you're talking about, too? Or did I again miss the point?
All this is part of the paradox that @Sascha hinted at time and again: that placing notes carefullt, e.g. in a hierarchy where the place is encoded in the ID, will lead to the hierarchy becoming irrelevant. Cross-references or links accelerate this process even more, because with links, you don't have to rely on the placement, so you will eventually care less and less.
Author at Zettelkasten.de • https://christiantietze.de/
I think we're in agreement here: a system of "multiple branching" has no obvious advantage over a system with only binary branching.
YES! YESSSsssssss!!! 🥳
Author at Zettelkasten.de • https://christiantietze.de/