Using a zettelkasten in mathematics research
@bradfordfournier wrote here:
Any shared experiences re mathematics research in your zettelkasten would be great.
I think this deserves a discussion of its own, with a more telling title than the one where it came up.
@bradfordfournier - I hope you are OK with this.
Howdy, Stranger!

Comments
Of course. Thanks.
Side note on quickly getting some latex into your editor / zk :
One external piece of software / app that I've found incredibly helpful is the iOS app "Snip" which takes a picture of some mathematics and converts via ocr, to latex in multiple formats. It's excellent with hand-written OCR as well.
Attached is the image taken of a simple bit of math and the app interface which provides the result.
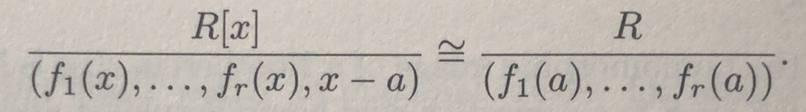
The result provides multiple formats as well as the confidence in the OCR. It can handle much more complex images including category theory etc. Very helpful for quickly getting some math into your preferred editor / zk software.
My current ideas on paper-ZK-based problem solving is outlined here, and the crucial question to me seems that of problem solving tools: Which tools are the most useful, given one's mathematical domain of work, knowledge, skills and expertise?
(In a way, I suspect the tool collection could be a kind of plug-in - you could have tool collections for maths, for physics, for philosophy etc., with a certain overlap in general methods and any amount of diversity in specific methods.)
Having a tool collection that can be adapted with ease and that co-evolves with its user seems of paramount importance.
The math tool collection from George Polya's "How to Solve It" is perhaps the most famous in mathematics, but personally, I never found it very helpful with its four stages of
1) Understanding
2) Making a Plan
3) Carrying Out the Plan
4) Looking Back,
and its heavy reliance on using "related problems" one had solved earlier.
I found the methods developed by Mason / Burton / Stacey in "Thinking Mathematically" and by Spyros Kalomitsines in "How to Solve Problems: New Methods and Ideas" much more accessible. Kalomitsines in particular gives a number of examples that show the interplay between thinking tools and "writing for insights" in the process.
In my years of study and at my university, there was practically no instruction about the methodology of problem solving, and although I had a number of friends that were really good at maths, there was little informal talk about methods.
Even in retrospect, I cannot describe the reasons for this.
I think that even a very small community of ZK users communicating about their experiences could profit considerably. Given an explicit framework of concepts on how to write work notes, how to organize notes, how to use tools would enable them to progress decently - by discussing questions like
how do you deal with confusion,
what do you try when you are stuck,
how do you generate new approaches,
how do you organize your tree of solution trials" etc.
Here's a passage from a 1984 interview with Michael Atiyah:
The essay examines differences between "problem solvers" and "theory builders".
I'm mentioning it here because Atiyah's approach seems to correspond to straightforward zettelkasten work.
About his own work habits, Atiyah said:
Not exactly the principal witness for my "write for insights" mantra, as it seems.
@thomasteepe
Great quotes. And while he may not be the poster boy for "write for insights" he is the poster boy for "walk for insights". I still think putting the two together is a dynamite combination.
Here's advice by Terence Tao on "Write down what you've done".
On his page "What's new" he has subsections on "Career Advice" and "On Writing".
There is no explicit connection to zettelkasten work, but tons of good advice on doing and on writing maths that can be used in any form of organizing knowledge.
One of the most relevant discussion on mathoverflow.net (a question and answer site for professional research mathematicians) seems to be "How do you keep your research notes organised?"
The discussion was closed 9 years ago, with the following howler of an argument:
There are 16 answers, mentioning paper notebooks, TeX files, wikis, photos of handwritten notes in Evernote, etc. I'm pretty sure that many of the commenters back then would agree today that a zettelkasten, digital or perhaps paper-based or hybrid, would provide a compelling basis for their work.
@GeoEng51
At this very moment, I'm looking for information about how mathematicians organise their work.
Here's something from an interview with Andrew Wiles.
Here are some miscellaneous first ideas that seem useful to me in dealing with problem solving in a zettelkasten.
I'm afraid it's a bit abstract and theoretical, but giving compelling examples is not easy - so I start with the following remarks.
There is a large number of general or specific approaches I can try, like "dissect the problem into smaller parts", "look at special cases, look at extreme cases, look at limit cases etc." or "I know a somewhat similar problem and its solution from the past - perhaps I can use that here" or "Here's a paper that seems relevant - can I actually use it to make progress?".
I can use an externalized tool collection (or suitable mnemo techniques or checklists) to make the exploitation of standard approaches more reliable.
Exploiting these approaches will often lead to notes that primarily emerge as paths and trees and that can be otherwise cross-linked in the usual ZK fashion. Many of these paths will end without a clear result - I have to abandon them rather than being able to finalize them.
In some cases these paths will lead to important sub-problems where I can use a similar dossier structure for their examination.
It might be useful to centralize the process of generating further approaches to a solution.
In the spirit of Spyros Kalomitsines' method "Getting out of loops", I can try to form negations to the approaches I've tried so far.
In many situations I will have a bundle of approaches, some promising and some too far-fetched to be worthy of close examination.
To me it seems natural to find ways of doing some "housekeeping" on various items - like how to deal with approaches that could be examined later, how to deal with abandoned paths, etc.
Let's see an example.
I gave an example in another thread: formalizing Niklas Luhmann's Folgezettel, at least to within substitution of numbers for alphabetic characters. I wanted to make the case that verbal descriptions of theories tend to be too imprecise to be useful. They often admit interpretations that formal accounts exclude. Verbal argumentation to that effect has no traction. An example is needed. I wanted to settle arguments. The "antinet" argument, specifically.
The punchline: anything digital timestamp IDs can do, general Folgezettel IDs can do, and conversely. There is a procedure for adding structure notes to a (digital) ZK with links aliased to (or defined by) Folgezettel IDs.
Because of the potential for loss of information (the direction from digital timestamp IDs to Folgezettel is the more difficult to control), it's a good idea to decide on one scheme from the outset, (or do both at once, which is possible).
With Folgezettel, you have a procedure for defining structure notes; without them, you're on your own. It takes judgment, which I obviously lack. I'm inclined to add Folgezettel to YAML keyword blocks in my digital ZK with timestamp IDs to make structure notes easy to build in. But that's an experiment in "Luhmannization."1
The math was induction over strings, essentially. Some care was needed stating definitions—in combinatorics, overlooking cases is common. There was one combinatorial fact, an order-preserving map used to define a linearization of a partial order. You can see my mistakes, typos, dead ends, laziness that had to be overcome. At this stage I don't care: the point is to record your thought process in a format that facilitates improvement. Keep a record of what doesn't work--by leaving your notes in the ZK where they lie. The Zettelkasten format didn't get in the way, on the contrary. It works, or can be made to work for mathematical problem solving.
By the way, I ordered a book of Luhmann's on systems theory, specifically social systems. It's not mathematical, but I would not be so quick to dismiss what Luhmann says because it is a verbal description of a theory. A certain well-known economist I met years ago wasn't impressed with Luhmann. Nevertheless, I have the same nagging sense that I had with the Folgezettel, which is that it admits a formal, applicable mathematical interpretation. It need not be particularly deep mathematics--the standard is empirical validity. Luhmann criticizes social science for its anthropocentrism. He's not a methodological individualist (clarifying this takes work, since there are several types of methodological individualism). He also makes certain remarks about the political and economic "systems" (to name two) that remind me of Craig's Theorem in mathematical logic. So at least you can find mathematical consistency, if you look. I suspect there is more to it. ↩︎
GitHub. Erdős #2. Problems worthy of attack / prove their worth by hitting back. -- Piet Hein. Alter ego: Erel Dogg (not the first). CC BY-SA 4.0.
@ZettelDistraction:
I reread Andy Matuschak's great sobering note "People who write extensively about note-writing rarely have a serious context of use" from time to time.
I still hope there is some value in discussing writing-based and ZK-based methods of solving hard problems.
At this moment, I cannot assess the usefulness of extending maps to monoid homomorphisms for zettelkasten work.
Mathematician Raoul Bott said:
In the above model of a "vertical" main axis of starting points / approaches and of "horizontal" paths or trees that exploit these approaches, we can separate two types of persistence - one for generating approaches, and one for examining them.
Both types of persistence can be supported by a substantial set of fairly specific externalizable operational tools.
Are you suggesting that my example wasn't hard?
That's a mischaracterization, but it's understandable. The Bach cantata is gorgeous—now show your work! Insubstantial work will suffice—Ach wie flüchtig, ach wie nichtig.
I've met some great and very fine mathematicians myself. Jardine told me that there is no right way to do mathematics.
I'm really a hobbyist at this point.
GitHub. Erdős #2. Problems worthy of attack / prove their worth by hitting back. -- Piet Hein. Alter ego: Erel Dogg (not the first). CC BY-SA 4.0.
@ZettelDistraction wrote:
In my view discussions of such processes are underrepresented in this forum, given their potential.
(Again: Let's not forget that the majority of breakthrough insights in history was made without the use of ZKs - is there something we can learn from that?)
(In my view, one obvious deficit is a lack of methods for quickly and thoroughly forming an understanding of math concepts from talks and texts - I found @bradfordfournier's post here quite illuminating.)
I apologize.
More than a few successful researchers rely on their filing cabinets, to which Luhmann's Zettelkasten bore a striking resemblance. Here I am not trivializing the search for methods–I recall, probably mistakenly, reading about the utility of filing cabinets for mathematical research on Terence Tao's blog, but I am having difficulty locating it. He has excellent career advice (which I am sure you are aware of). I doubt I measure even one femto-$(\tau)$ in ability.
Ignore the trollface emoji.
emoji.
My impression was that the literature on this is immense, with significant grant funding available, at least in the US. Grant procurement for academic physics education strikes me as a racket.
Speaking of being "... stupider than everybody else -- but persistent," there is The Importance of Stupidly in Scientific Research.
No need to apologize. I should apologize.
GitHub. Erdős #2. Problems worthy of attack / prove their worth by hitting back. -- Piet Hein. Alter ego: Erel Dogg (not the first). CC BY-SA 4.0.
Here is another perspective on ZK-based problem solving in maths.
I know that a model like the following is too neat, and that actual problem solving is messy. Again, I see this as a first collection of building blocks.
If discussions here lead to different sets of building blocks in different combinations based on different premises, I am more than happy.
Step 1:
State the problem.
Step 2:
Find a heuristic plan that promises progress on the problem solution.
Step 3:
Find an operator that fits into the heuristic plan and that can be applied to the problem situation.
Step 4:
Apply the operator to the problem situation and write down the insights stimulated by the operator.
Step 5:
Incorporate the relevant insights from those responses into your web of notes on the problem.
Step 6:
If the problem is not yet solved, go back to step 3 until the heuristic plan is exhausted.
Step 7:
If the problem is not yet solved and the heuristic plan from step 2 is exhausted, go back to step 2 - as long as further work on the problem seems promising.
Obviously I have left out countless refinements - rules of thumb for abandoning work on one approach, rules of thumb for abandoning a problem altogether, options for parallel work on several heuristic plans and several operators etc, and the demarcation between heuristic plans and operators is often blurry.
But even in its present crudeness, I hope this model allows some discussions.
(The model is influenced by the flow diagrams in Dietrich Dörner's 1976 book Problemlösen als Informationsverarbeitung.)
Here are ideas and examples to find a set of useful actionable practices for the above steps.
For each step, we can ask for possible practices adapted to math problem solving and for possible ZK-related practices.
For step 1:
State the problem.
Possible math practices:
Sometimes, we can start with a rigorous statement of the problem, in other cases, a first version of the problem may be not much more than a hunch - I see developing a more precise formulation as part of the problem solving process.
Possible ZK practices:
Writing a note with the initial problem seems an obvious starting point.
For step 2:
Find a heuristic plan that promises progress on the problem solution.
Possible math practices:
Here are some examples of math-related heuristic plans: Polya's four stages scheme from "How to Solve It", Kalomitsines' spiral method with its three components description method, means-ends-analysis and getting out of loops - more here. Furthermore, strategies of forward search and backward search, and a number of general proof techniques like induction or proof by contradiction.
In many cases, different heuristic plans like these will have connections or overlaps, or they will consist of similar building blocks.
Possible ZK practices:
We can establish a library of heuristic plans and of building blocks of heuristic plans. As stated elsewhere, I've experienced differences between plans that are buried in the zettelkasten and have to be accessed with some effort and those that are visible with one glance.
For step 3:
Find an operator that fits into the heuristic plan and that can be applied to the problem situation.
Possible math practices:
Here are some examples of math-related operators: Looking for symmetries, patterns, limits, extremal cases, invariants. Using general math tools like generating functions. Applying inequalities, theorems etc.
A special case of operators are different representations - via different diagrams, math terms or perhaps algorithms. Different representations can lead to different operators that can be applied to a problem.
In many cases, it's useful to find a suitable math notation for the entities in the problem.
Possible ZK practices:
As with the heuristic plans from step 2, operators can be organized in libraries. It seems promising to find links between certain problem situations and operators that can help resolving them. The Tricki has used a number of ideas to organize problem solving tools and operators.
For step 4:
Apply the operator to the problem situation and write down the insights stimulated by the operator.
Possible math practices:
Part of this is arguably the kind of work many people will associate with maths first - writing down equations and transforming them, solving integrals, drawing diagrams etc. My personal favourite for this are ways of "writing for insights" where reflection and reorientation are built into the writing process - for a possible candidate see here.
Moreover, we can experiment with writing processes that focus on creating first ideas on a larger set of stimuli, like here. But, again, these are experiments with little evidence of their usefulness, so people may want to work with more conventional methods.
Possible ZK practices:
The "writing for insights" in this step is crucial - and yet of a temporary kind. It seems reasonable (but certainly not mandatory) that these notes stay outside the regular zettelkasten.
For step 5:
Incorporate the relevant insights into your web of notes on the problem.
Possible math practices
There are established methods of dividing complex proofs into smaller units by using overviews, lemmata, etc.
Possible ZK practices:
For those insights from step 4 that do not yet fit into a larger framework of a proof, we can use the "main axis" concept from this previous post, and later use these items to build proofs.
Crosslinks to other notes, perhaps on other problems, are part of regular ZK work.
Steps 6 and 7 are of a general nature - at present, I have no concrete ideas on specific math practices or ZK practices for them.
My main point with all this is to outline a ZK-based, maths-related framework that supports coherent systematic work on a hard problem over a large number of different approaches.